
When we do linear regression, we assume that the relationship between the response variable and the predictors is linear. If they fall above 2 or below -2, they can be considered unusual.Ģ.1 Tests on Nonlinearity and Homogeneity of Variance Testing Nonlinearity If residuals are normally distributed, then 95% of them should fall between -2 and 2. Standardized variables (either the predicted values or the residuals) have a mean of zero and standard deviation of one. Here is a table of the type of residuals we will be using for this seminar: Keyword Our goal is to make the best predictive model of academic performance possible using a combination of predictors such as meals, acs_k3, full, and enroll. We will use the same dataset elemapi2v2 (remember it’s the modified one!) that we used in Lesson 1.
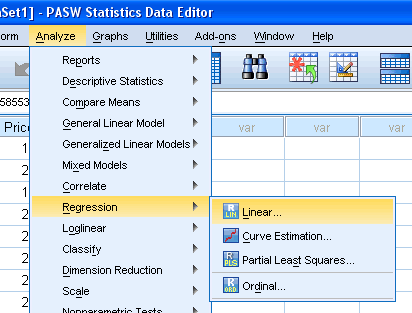
LINEAR REGRESSION SPSS HOW TO
In this lesson, we will explore these methods and show how to verify regression assumptions and detect potential problems using SPSS. Many graphical methods and numerical tests have been developed over the years for regression diagnostics and SPSS makes many of these methods easy to access and use.
Multicollinearity – predictors that are highly related to each other and both predictive of your outcome, can cause problems in estimating the regression coefficients.Model specification – the model should be properly specified (including all relevant variables, and excluding irrelevant variables)Īdditionally, there are issues that can arise during the analysis that, while strictly speaking are not assumptions of regression, are nonetheless, of great.Independence – the errors associated with one observation are not correlated with the errors of any other observation.Normality – the errors should be normally distributed – normality is necessary for the b-coefficient tests to be valid (especially for small samples), estimation of the coefficients only requires that the errors be identically and independently distributed.Homogeneity of variance (homoscedasticity) – the error variance should be constant.Linearity – the relationships between the predictors and the outcome variable should be linear.In particular, we will consider the following assumptions. Since we have 400 schools, we will have 400 residuals or deviations from the predicted line.Īssumptions in linear regression are based mostly on predicted values and residuals. In this particular case we plotting api00 with enroll. Predicted values are points that fall on the predicted line for a given point on the x-axis. The residual is the vertical distance (or deviation) from the observation to the predicted regression line. The observations are represented by the circular dots, and the best fit or predicted regression line is represented by the diagonal solid line. Let’s take a look a what a residual and predicted value are visually: Which says that the residuals are normally distributed with a mean centered around zero. Recall that the regression equation (for simple linear regression) is:Īdditionally, we make the assumption that This lesson will discuss how to check whether your data meet the assumptions of linear regression. Standard errors (e.g., you can get a significant effect when in fact there is none, or vice versa). In a similar vein, failing to check for assumptions of linear regression can bias your estimated coefficients and Without verifying that your data has been entered correctly and checking for plausible values, your coefficients may be misleading. In our last lesson, we learned how to first examine the distribution of variables before doing simple and multiple linear regressions with SPSS. 2.1 Tests on Nonlinearity and Nonconstant Error of Variance.


 0 kommentar(er)
0 kommentar(er)
